

According to the last image, it is better to use either the Forward or the Backward algorithm.
The probability over the best Viterbi path is a "cheap" alternative to the real solution.

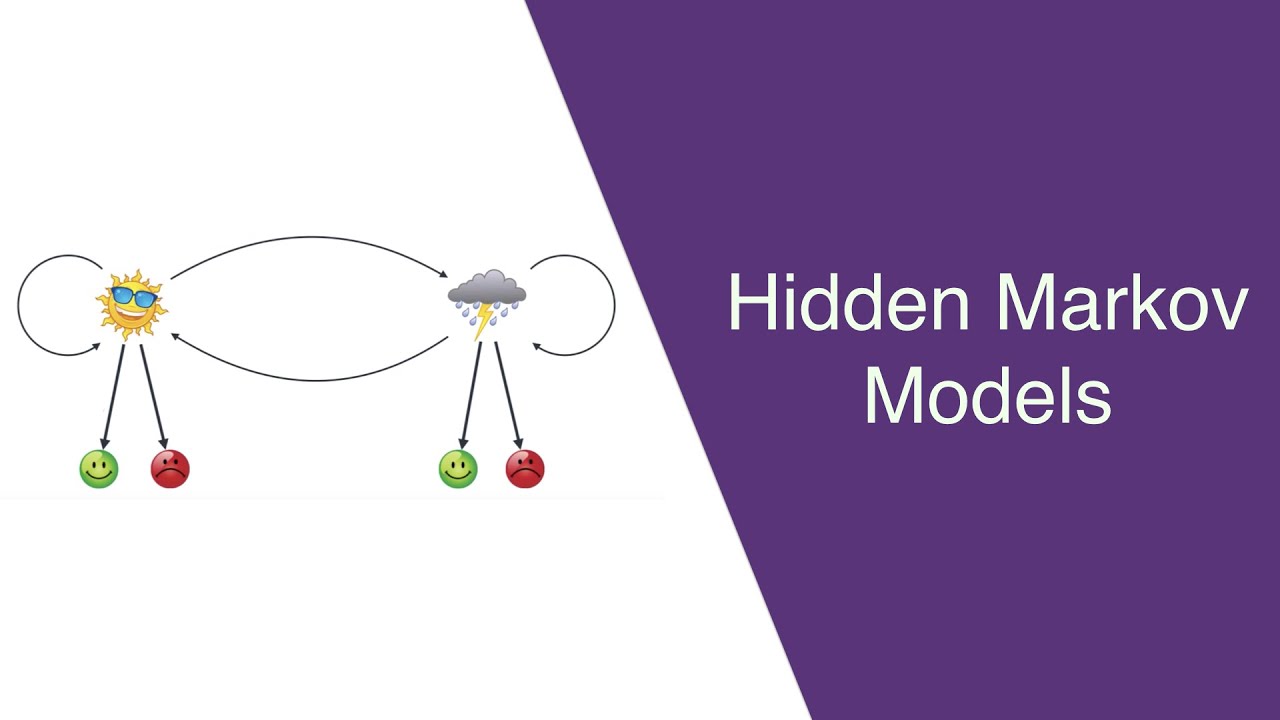
You want to see which out of 2 models scores higher:īecause i've used two hmms for each obsv sequence and i want to see which hmm is the winner or best matches. This will give you a score, for sure, but I am not convinced if this is the best solution for the second part of your question. Where you simply have to multiply the emission and the transition probabilities. given a model $M$, a single path $π$ and a set of observations $x$, what is the actual joint probability of the path and the observations, if we know the model? You are trying to solve this: This looks like you are asking for a solution to problem 1 here, i.e. Is there any way to derive the probability (score) of this calculated state sequence from the hmmviterbi code available in matlab or any other algorithm? I think you might be confusing 2 separate things here, but have a look at the following images before I try to explain my thinking and focus on the Scoring rows:


 0 kommentar(er)
0 kommentar(er)
